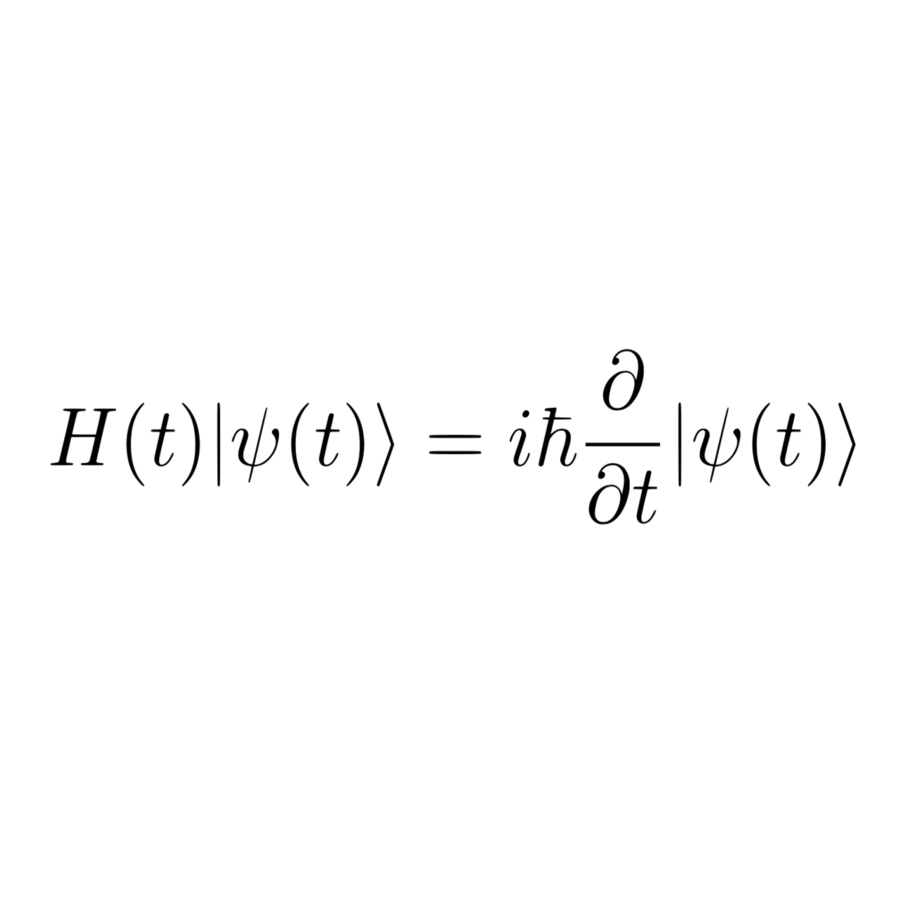Graph Theory and Quantum Entropy
Amherst College
Summer 2019
TEAM MEMBERS: Maria-Cristiana Gîrjău, Andrew Moore, Andrew Rosevear, Matthew Sanders,
Andrew Tawfeek, Dawit Wachelo
FACULTY SUPERVISOR: Prof. Ivan ContrerasSee personal webpage
PROJECT OVERVIEW
The objective of this Summer Research Project is to study the link between various concepts in Mathematical Physics such as entropy, quantum states, Schrödinger's equation, etc. and Graph Theory. We are exposed to networks in our every-day life: social networks, airports, road maps, the Internet... Some questions appear naturally:
- How complex is the network?
- How many different paths do we have to go from one place to another?
- How efficiently does information travel through the network?
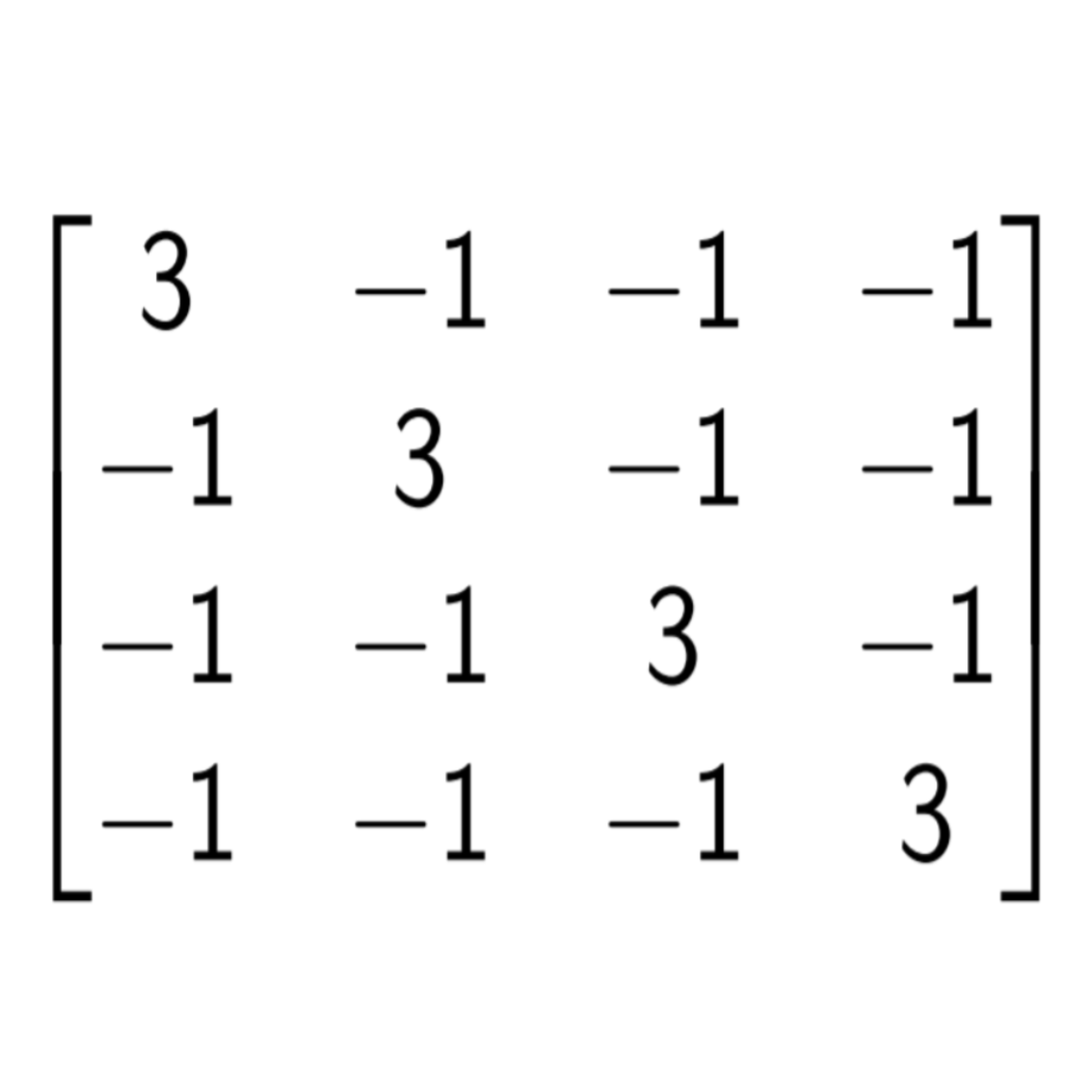
It turns out the Graph Laplacian provides answers to some of these questions! By using the techniques of Mathematical Physics and Statistical Analysis, we intend to explore further the connection between quantum mechanical systems and Graph Theory.
VISUALIZATIONS
The Phase Space Visualization of Schrödinger's Equation
Phase space is an imaginary “space” representing the system. The state of the system is represented as a single point. For a graph with \(n\) vertices at time \(t\), \(\Psi\) is an \(n-\)dimensional complex vector. Therefore the state is a unique point in \(2n-\)dimensional real space. Schrödinger's equation describes the movement of that point.
Instructions:
Schrödinger's Equation on a Graph
*Andrew Moore is still working on it*
CODE
Macaulay 2
Read more about the Macaulay2 language here.
You can compile and run Macaulay2 code in the browser here.
How to use the Macaulay2 code:- Copy and paste all of Macaulay2_Code.txt into Macaulay2 and hit enter. Wait roughly ~10 seconds until there's an Output and it's done compiling.
- Enter graph as follows: for the case of, say, a "triangle", we have:
- V = {a, b, c} --hit enter
- E = {(a, b), (b, c), (c, a)} --hit enter
- G = (V, E) --hit enter
- Now G denotes your graph and you may use the following commands. Everywhere G is mentioned, it is referring to the above definition.
Command Documentation
Click on any command to view details about its usage.
- G, a Sequence (as defined above)
- vertexassignments, a List, the list of assignments to vertices for the discrete function
- edgeassignments, a List, the list of assignments to edges for the discrete function
- N/A
- This creates a discrete function on the vertices of a graph.
- (v, 0), a Sequence, where v is a vertex of the graph G
- (v1, v2), a Sequence, where (v1, v2) is an edge of the graph G
- Evaluation of the discrete function assigned on the graph G at the vertex v or edge (v1, v2)
- Must use assign function before using this.
- G, a Sequence (as defined above)
- fn, a discrete function (just enter fn if assignment already provided)
- (v, 0), a Sequence, where is a vertex of the graph G OR (v1, v2), a Sequence, where (v1, v2) is an edge of the graph G
- Provides the Morse set (class List) for a single vertex or edge of G under the assignment provided. Note that only one set is output, as the other set for either an edge or vertex is always empty (due to the ordering on the union of V and E)
- G, a Sequence (as defined above)
- fn, a discrete function (just enter fn if assignment already provided)
- Output true if discrete function is Morse, false if not Morse.
- G, a Sequence (as defined above)
- fn, a discrete function (just enter fn if assignment already provided)
- The critical points (vertices and edges) of G (class List).
- G, a Sequence (as defined above)
- fn, a discrete function (just enter fn if assignment already provided)
- The HyperGraph (class) formation of G.
- Very useful! Allows one to use all the commands found here with the Output: Commands
- G, a Sequence (as defined above)
- fn, a discrete function (just enter fn if assignment already provided)
- The Graph (class) formation of G.
- Very useful! Allows one to use all the commands found here with the Output: Commands
- G, a Sequence (as defined above)
- The adjacency matrix of G (class Matrix).
- G, a Sequence (as defined above)
- The incidence matrix of G (class Matrix).
- G, a Sequence (as defined above)
- The even Laplacian of G (class Matrix).
- G, a Sequence (as defined above)
- The odd Laplacian of G (class Matrix).
- G, a Sequence (as defined above)
- The cohomology group \(H^0\) of G (class Module).
- G, a Sequence (as defined above)
- The cohomology group \(H^1\) of G (class Module).
- G, a Sequence (as defined above)
- The 0th Betti number of G (class Element).
- G, a Sequence (as defined above)
- The 1st Betti number of G (class Element).
- n, an Element (i.e. a number)
- An \(n \times n\) identity matrix (class Matrix).
- M, a Matrix
- A matrix with domain and range expanded from integers to the complex numbers (class Matrix).
- M, a Matrix
- A matrix with domain and range expanded from integers to the rational numbers (class Matrix).
- M, a Matrix
- order, an Element (i.e. a number)
- The exponentiation of the matrix M to the order given (class Matrix).
- G, a Sequence (as defined above)
- The Euler characteristic of the graph (class Element).
- G, a Sequence (as defined above)
- The spectrum of the even Laplacian (class Matrix).
- G, a Sequence (as defined above)
- The spectrum of the odd Laplacian (class Matrix).
- G, a Sequence (as defined above)
- H, a Sequence (as defined above) (another graph)
- The Kronecker product of the two graphs (class Matrix).
Mathematica
PRESENTATIONS
Conference for New England REUs (UMASS Amherst, July 2019)
Quantum Graph Entropy and the Phase Space Visualization of Schrödinger's Equation
(Gîrjău, Moore, Wachelo)
ABSTRACT: Von Neumann Graph Entropy (VNGE) is a measure of the complexity of a graph calculated using the spectrum of the graph Laplacian. Here, we shall present a brief overview of the underlying theory, some proven results and various approximation methods for VNGE. We then discuss the phase space representation of the Schrödinger equation for graphs and its visualization, as well as ongoing work on the periodicity of the solutions.
Graph Topology and Discrete Morse Theory
(Rosevear, Tawfeek)
ABSTRACT: One can adapt the tools of algebraic and differential topology to study topological properties of the graph, such as number of cycles and connected components. We use the graph chain complex and homology to motivate and define the even and odd graph Laplacians and graph de Rham calculus. We then present discrete Morse theory on a graph, including an equivalence class of Morse functions that gives rise to a simple proof of the Morse inequalities. Further directions include generalization to CW complexes, application of discrete differential forms to problems in graph quantum mechanics, and finding a closed form expression for the number of Morse equivalence classes on a given graph.
Southeastern Undergraduate Mathematics Workshop (Georgia Tech, August 2019)
Faculty Presentations (Amherst College, August 2019)
The Mathematics of Quantum Mechanics and Networks
(Prof. Ivan Contreras)
ABSTRACT: Mathematical Physics is a fascinating area of science that brings together different perspectives on how we understand the Physics that rules our world. This talk provides a gentle overview of a graph theoretical model of Quantum Mechanics, as an example of how we can use tools from Linear Algebra and Calculus to understand the basic principles of Quantum Mechanics.
Mathematics Undergraduate Colloquium (Yale University, August 2019)
Quantum Mechanics and the Shape of Graphs
(Prof. Ivan Contreras)
ABSTRACT: Quantum Physics has revolutionized the way we understand our world. Since the beginning of the 20th century, beautiful Mathematics has been devised and implemented in order to achieve such success. This talk intends to give an overview of a discretized model of Quantum Mechanics: the Schrödinger equation on graphs. We will use the combinatorial graph Laplacian to describe certain properties of finite graphs such as topological invariants, number of generalized walks, and entropy. No prior knowledge of Physics or Graph Theory will be assumed.
REFERENCES
[1] Minello, Giorgia, et al. On the Von Neumann Entropy of Graphs, Journal of Complex Networks, no. 00, 23 Jan. 2018, doi:10.1093/comnet/cny028.
[2] C. Yu. Superwalk Formulae for Even and Odd Laplacians in Finite Graphs Rose Hulman Undergraduate Mathematics Journal: Vol. 18: Iss. 1, Article 16 (2017)
[3] F. Sanchez. Eigenvalues and Eigenvectors of Subdirect Sums Proceedings of the 9th WSEAS International Conference on Applied Mathematics, Istanbul, Turkey (2006)
[4] I. Contreras, B. Xu. The Graph Laplacian and Morse Inequalities Pacific Journal of Mathematics, Vol. 300 (2019), No. 2, pp. 331-345
[5] L. Han, E. Hancock, R. Wilson. Characterizing Graphs Using Approximate von Neumann Entropy Pattern Recognition and Image Analysis (2011), pp. 484-491
[6] R. Forman. A User’s Guide to Discrete Morse Theory Śeminaire Lotharingien de Combinatoire 48 (2002)